【numpy】多次元離散フーリエ変換/逆変換

【numpy】多次元離散フーリエ変換/逆変換
2020年2月20日
少し前、Pythonのモジュールnumpyの離散フーリエ変換・逆フーリエ変換のfftn・ifftnの挙動が全く分からず1ヶ月ぐらい泥沼にハマった。
今考えれば何であんなに詰まっていたかよくわからないけども、いきなり多次元で扱うには公式の説明では足りないかなと思ったので、今後使う人の参考にでもなればと思います。
公式の説明はこちら
https://docs.scipy.org/doc/numpy/reference/generated/numpy.fft.fftn.html
配列を途中で折り返すことやら配列の0番目の要素に対応する要素が無いことやらは分かるかもしれないけれども直感的にイメージしずらいかと。
厄介なのはこれを多次元に拡張したとき。これにハマった。
とりあえず大切なことは
波数配列を普通の数直線状に作らないこと
です。
スポンサーリンク
一次元離散変換
波数空間から実空間に戻す方がなんとなくイメージしやすかったので逆変換していきます。
別にフーリエ変換もやることは一緒なので、fft使う場合も同じことやってください。
さて、まずは1次元での逆変換を見ていきましょう。
波数並列を作るわけだけども、要素数nが偶数か奇数かで話が変わります。
nが奇数の場合
まず0番目の要素に波数0が入る。
これは奇数でも偶数でも同じである。
1から(n-1)/2番目には正の波数、(n-1)/2+1からn-1番目には負の波数が入る。
負の波数は(n-1)/2+1番目に一番小さな波数(絶対値が一番大きな波数)を入れる。
例として要素数が7個の配列を考えてみる。
| 配列番号 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 波数 | 0 | 1 | 2 | 3 | -3 | -2 | -1 |
正負全ての波数がお互いに対応し合う。
nが偶数の場合
奇数の時と同じように0番目には波数0が入る。
また、1からn/2番目には正の波数、n/2+1からn-1番目には負の波数を入れる。
例えば要素数8個の場合
| 配列番号 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 波数 | 0 | 1 | 2 | 3 | 4 | -3 | -2 | -1 |
となる。
正の波数の要素数が負の波数より1個多くなり、n/2番目(正の最大波数)と対応する負の波数が無くなる。
Gaussianの1次元フーリエ逆変換実装
試しに波数空間でのgaussianを実空間でのgaussinに変換してみましょう。
gausianなら波数空間と実空間で形が変わらないので分かりやすい。
フーリエ変換でも逆変換でもやり方は同じです。
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
x = np.arange(-5,5,0.1)
gaussian = norm.pdf(x,0,1) #Gaussian生成
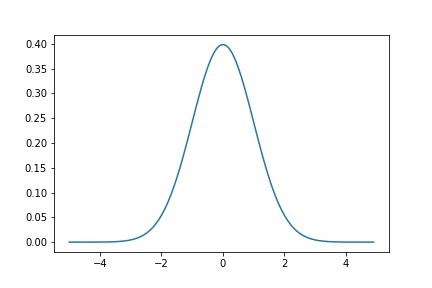
まず元となるGaussianを生成しました。
逆変換することによって幅は狭くなり高さも小さくなるが、変換後もこんな感じのものが出力されたら成功ですね。
n=len(gaussian)
gaussian_posi = gaussian[:int(n/2)-1] #正の波数
gaussian_nega = gaussian[int(n/2)-1:] #負の波数
change_gaussian = np.concatenate([gaussian_posi,gaussian_nega]) #ifft用に並べ替え
real_gaussian = np.fft.ifft(change_gaussian) #フーリエ逆変換
real_posi = real_gaussian[:int(n/2)-1]
real_nega = real_gaussian[int(n/2)-1:]
real_1 = np.concatenate([real_nega,real_posi]) #出力配列を数直線に対応するよう並べ替え
x = np.arange(-5,5,0.1)
plt.plot(x,real_1)
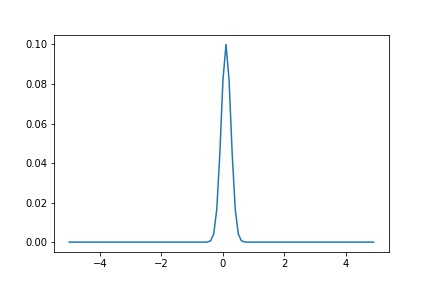
Gaussianっぽいものが出てきました。上手くいってそう。
ここで注意が必要なのは逆変換による出力配列も入力波数配列のように[0→正,負→]となっているので、実空間の数直線に対応した配列に並び替えなければいけないということを忘れないでください。
スポンサーリンク
多次元離散変換
2次元の変換はfft2・ifft2、多次元変換はfftn・ifftnであり、多次元変換では入力配列からnumpyが勝手に何次元変換かを判断してくれる。
多次元配列の対応関係
軸の作り方は1次元の時と同じです。
しかし配列の組み方が少しややこしいです。
波数0の点や、Nが偶数の時にN/2の要素を0に置き換えることは変わりません。
ただしkx-ky-kz空間のN×N×N配列で[a,b,c]と対応する要素を[N-a,N-b,N-c]とするとハマります。
ここでは軸上・平面上・ その他の点で場合分けをする必要があります。
軸上の点
$$kx\neq0,ky=0,kz=0$$
$$kx=0,ky\neq0,kz=0$$
$$kx=0,ky=0,kz\neq0$$
この時対応し合う要素は、それぞれの軸上で対応させます。
例えば[a,0,0]というkx軸上の点は[N-a,0,0]と対応します。
ky,kz軸上の点も同様です。
平面上の点
$$kx\neq0,ky\neq0,kz=0$$
$$kx=0,ky\neq0,kz\neq0$$
$$kx\neq0,ky=0,kz\neq0$$
この時は各平面上で対応させます。
例えば[a,b,0]というkx-ky平面上の点は[N-a,N-b,0]と対応します。
他の平面も同様です。
その他の点
$$kx\neq0,ky\neq0,kz\neq0$$
この場合は[a,b,c]と対応する点は[N-a,N-b,N-c]となります。
これは1次元の時を思い出せばイメージしやすいかと思いますが、これと同じことを軸上や平面上の点にも適応させてしま
3次元のフーリエ逆変換実装
こちらも実際にやってみましょう。
今回実験としてやる内容は
①[kx,ky,kz]の配列のうち、kz≥0の領域を適当な乱数に適当な位相をかけて作る
②kz<0の領域は、①で作ったものを実際の3次元波数空間(ifftn用に並べ替えた空間ではない)で原点対象になるように複素共役を取るように作る
③ifftnで実空間に戻す
ということをやってみようと思います。
イメージしずらいと思うので、具体的にはkz≥0で
$$\delta(\vec{k})=Acos\theta+iBsin\theta$$
を作り、kz<0ではこれを使って複素共役を取り
$$\delta(-\vec{k})=Acos\theta-iBsin\theta$$
を作っていきます。
なぜ今回これをするかというと、フーリエ逆変換はkと-kの波数の足し合わせですので、変換後虚部が消えていれば上手くいっていると分かるからです。
(※注:実際は離散変換なので変換後虚部が残りますが、実部と比べて桁がものすごく小さいです)
まあこれは理解するための練習なので、自分で理解できたら用途に合わせた実装をしてください。
import numpy as np
bin = 64
grid = bin*2 #1方向の要素数
k_posi = np.arange(0,bin,1)
k_nega = np.arange(-bin,0,1)
k = np.hstack((k_posi, k_nega))
k_vec = np.array([k,k,k])#3次元波数ベクトル
せっかくなので乱数は波数依存性を持つ正規分布乱数で作っていきます。
np.random.seed(0)
k_plane = np.zeros((grid,grid,grid),dtype=complex)
for k in range(bin):
for j in range(grid):
for i in range(grid):
#原点
if i == 0 and j == 0 and k == 0:
k_plane[i,j,k] = 0
#軸上の数値生成
#kz軸上
elif i == 0 and j == 0 and k != 0:
theta = 2*np.random.rand()*np.pi
k_plane[0,0,k] = np.random.normal(0,np.sqrt(k_vec[0, i]**2 + k_vec[1, j]**2 + k_vec[2,k]**2))*np.exp(1j*theta)
k_plane[0,0,grid-k] = k_plane[0,0,k].conjugate() #複素共役
#ky軸上
elif i == 0 and j != 0 and k == 0:
theta = 2*np.random.rand()*np.pi
k_plane[0,j,0]= np.random.normal(0,np.sqrt(k_vec[0, i]**2 + k_vec[1, j]**2 + k_vec[2,k]**2))*np.exp(1j*theta)
k_plane[0,grid-j,0] = k_plane[0,j,0].conjugate()
#kx軸上
elif i != 0 and j == 0 and k == 0:
theta = 2*np.random.rand()*np.pi
k_plane[i,0,0] = np.random.normal(0,np.sqrt(k_vec[0, i]**2 + k_vec[1, j]**2 + k_vec[2,k]**2))*np.exp(1j*theta)
k_plane[grid-i,0,0] = k_plane[i,0,0].conjugate()
#平面状の数値生成
#kz-kx平面上
elif i != 0 and j == 0 and k != 0:
theta = 2*np.random.rand()*np.pi
k_plane[i,0,k] = np.random.normal(0,np.sqrt(k_vec[0, i]**2 + k_vec[1, j]**2 + k_vec[2,k]**2))*np.exp(1j*theta)
k_plane[grid-i,0,grid-k] = k_plane[i,0,k].conjugate()
#kx-ky平面上
elif i != 0 and j != 0 and k == 0:
theta = 2*np.random.rand()*np.pi
k_plane[i,j,0]= np.random.normal(0,np.sqrt(k_vec[0, i]**2 + k_vec[1, j]**2 + k_vec[2,k]**2))*np.exp(1j*theta)
k_plane[grid-i,grid-j,0] = k_plane[i,j,0].conjugate()
#ky-kz平面上
elif i == 0 and j != 0 and k != 0:
theta = 2*np.random.rand()*np.pi
k_plane[0,j,k] = np.random.normal(0,np.sqrt(k_vec[0, i]**2 + k_vec[1, j]**2 + k_vec[2,k]**2))*np.exp(1j*theta)
k_plane[0,grid-j,grid-k] = k_plane[0,j,k].conjugate()
#その他の点
else:
theta = 2*np.random.rand()*np.pi
k_plane[i,j,k] = np.random.normal(0,np.sqrt(k_vec[0, i]**2 + k_vec[1, j]**2 + k_vec[2,k]**2))*np.exp(1j*theta)
k_plane[grid-i,grid-j,grid-k] = k_plane[i,j,k].conjugate()
今要素数が偶数なので正の最大波数と対になるものがおらず、虚部が出現する原因となるので最大波数の要素は全て0に置き換えます。
for k in range(grid):
for j in range(grid):
for i in range(grid):
if i == bin or j == bin or k == bin:
k_plane[i,j,k] = 0
フーリエ逆変換します。
x_plane = np.fft.ifftn(k_plane)
#実際の3次元軸に対応した配列に直す
real_x_plane = np.zeros((grid,grid,grid),dtype=complex)
real_x_plane[:bin,:bin,:bin] = x_plane[bin:grid,bin:grid,bin:grid]
real_x_plane[:bin,:bin,bin:grid] = x_plane[bin:grid,bin:grid,:bin]
real_x_plane[:bin,bin:grid,:bin] = x_plane[bin:grid,:bin,bin:grid]
real_x_plane[:bin,bin:grid,bin:grid] = x_plane[bin:grid,:bin,:bin]
変換されたものの実数値の平均は
real_x_plane.real.mean()1.040458506658468e-08
また、虚部の絶対値の最大値は
abs(real_x_plane.imag).max()4.459839890476434e-19
11桁違うので上手くいったと言えるのではないでしょうか。
スポンサーリンク












