【Python】自力で重力波解析

【Python】自力で重力波解析
2020年2月24日自力で、自分のパソコンの上で重力波のデータ解析をしていきます。
重力波のデータ解析に必要なものはアメリカの観測所LIGOが公開してくれているので簡単にできます。
実際に観測されたデータからノイズを取り除き、予測波形と比較していきます。
前提知識
・高校物理の知識
・大学1,2年生でやるぐらいの数学の知識
・コードを見ればなにやってるかそこそこわかるぐらいのPythonの知識
・jupyter notebookの環境構築がしてある
スポンサーリンク
そもそも重力波って?
宇宙分野に興味がある方なら聞いたことがあるかもしれませんね。興味がない方は聞いたこともないかもしれません。
重力波とは”光速で伝わる時空の歪み”です。
何を言っているか理解し難いですよね。
堅い話をすれば、一般相対性理論では、質量があるものが存在するとその周りの時空が歪みます。
その質量が動くと、歪みが光速で伝播していくのです。
ちょうど水の中に指を入れてその指を動かしたらできる波のイメージです。
時空が歪むというと非現実的な感じがしますが、実は僕たちも時空を歪ませているし、動けば重力波が発生しています。
しかし、日常生活程度で出会う物の質量ぐらいが生じさせる重力波では小さすぎて感じることができません。
現在の最先端の技術を持ってしてでも、太陽質量の何十倍もの質量を持つブラックホール同士が融合する時に生じる重力波を検知することが精一杯です。
逆に物が動いた程度で一々時空が歪みを感じていたら発狂します。
使用する観測データ
重力波の観測データは、アメリカの重力波観測施設“LIGO(ライゴ)”がネット上で公開してくれています。なのでこのデータをありがたく使わせて頂きます。この中には一緒にPython用の解析コードも入っているため、それを元に進めていきます。(このサイトに書いたコードは、僕が少しいじっているのでLIGOが公開しているコードと少し違ったりします。結果等は変わりません。)
重力波の観測方法
重力波を解析する前に、必要な前提知識としてLIGOでの重力波の観測方法を知っておきましょう。
重力波を直接可視光で観測することは不可能です。
なのでマイケルソン干渉計を用いて間接的に観測しています。
LIGOはワシントン州にあるハンフォード観測所とルイジアナ州にあるリビングストン観測所を持っています。
それぞれに長さ4kmの真空管2本が直角方向に設置されており、マイケルソン干渉計の原理で干渉縞の観測を行なっています。
この真空管の長さが一定なら、干渉縞も一定のはずです。
しかし重力波の時空の歪みによって真空管の長さが変われば、光が進む距離が変わり干渉縞も変化します。
この干渉縞の変化から重力波を検出するわけです。


またハンフォード観測所とリビングストン観測所は3002km(光速で10ms)離れており、2つの観測所への重力波の到達時間の差から、重力波の発生源の位置を知ることができます。
スポンサーリンク
観測データの入手
では実際に公開観測データをダウンロードしてみましょう。
LIGOの公式ページからデータをダウンロードしてください。
下記サイトの”Download the data on a computer with a python installation”というセクション中の”LOSC_Event_tutorial.zip”からダウンロードできます。
https://www.gw-openscience.org/s/events/GW150914/LOSC_Event_tutorial_GW150914.html
ここからダウンロードしたファイルをjupyterにアップロードしましょう。
”Files”のページから右上の”upload”からjupyterにアップロードできます。
解析開始!
それでは早速解析を初めていきましょう!
アップロードしたファイルの中の”LOSC_Event_tutorial.ipynb”に解析のソースコードが入っています。
”LOSC_Event_tutorial.ipynb”では様々な解析をしていますが、今回は
観測データからノイズを除去して、予測データと比較する
ことを目標にしてやっていきます。
なので”LOSC_Event_tutorial”の中で新しいノートブックを作成してください。
ではまずは下準備です。
eventname = ''
eventname = 'GW150914'
make_plots = 1 #グラフplotするので1
plottype = "png" #png形式で出力、pdfもできるダウンロードしたデータには4回分の観測データが入っていますが、今回は’GW150914’というデータを使うことを宣言しました。
これは2015年9月14日に観測されたデータという意味です。
必要なパッケージ等を読み込んでいきます。
#解析に必要なライブラリのインポート
import numpy as np
from scipy import signal
from scipy.interpolate import interp1d
from scipy.signal import butter, filtfilt, iirdesign, zpk2tf, freqz
import h5py
import json
#プロットに必要なライブラリのインポート
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
import matplotlib.mlab as mlab
#重力波解析のための特殊メソッドが入っているreadligo.pyをインポート
import readligo as rl
次に今回使う’GW150914’に関するデータを持ってこれるように変数定義していきます。
また、H1、L1というのはそれぞれハンフォード、リビングストンでの観測データということです。今後も結構出てきます。
fnjson = "BBH_events_v3.json"
try:
events = json.load(open(fnjson,"r"))
except IOError: #必要なjsonファイルが見つからない時に出るエラー
print("Cannot find resource file "+fnjson)
print("You can download it from https://losc.ligo.org/s/events/"+fnjson)
print("Quitting.")
quit()
try:
events[eventname]
except: #解析するデータを指定できていない時に出るエラー
print('You must select an eventname that is in '+fnjson+'! Quitting.')
quit()
event = events[eventname]
fn_H1 = event['fn_H1'] #ハンフォードでの観測データ
fn_L1 = event['fn_L1'] #リビングストンでの観測データ
fn_template = event['fn_template'] #'GW150914'での予測波
fs = event['fs'] #サンプリングレート
tevent = event['tevent'] #重力波が発生した時刻
fband = event['fband'] #バンドパスでの周波数帯
print("Reading in parameters for event " + event["name"])
print(event)
try:
strain_H1, time_H1, chan_dict_H1 = rl.loaddata(fn_H1, 'H1')
strain_L1, time_L1, chan_dict_L1 = rl.loaddata(fn_L1, 'L1')
except: #データが読み込めなかった時に出るエラー
print("Cannot find data files!")
print("You can download them from https://losc.ligo.org/s/events/"+eventname)
print("Quitting.")
quit()
これを実行すると以下の結果が出力されると思います。
‘GW150914’の解析に必要なデータを読み込めました。
また、サンプリングレートとは1秒間に何回記録するかをということです。(今回は4096Hz)
Reading in parameters for event GW150914
{'name': 'GW150914',
'fn_H1': 'H-H1_LOSC_4_V2-1126259446-32.hdf5',
'fn_L1': 'L-L1_LOSC_4_V2-1126259446-32.hdf5',
'fn_template': 'GW150914_4_template.hdf5',
'fs': 4096, 'tevent': 1126259462.44,
'utcevent': '2015-09-14T09:50:45.44',
'm1': 41.743,
'm2': 29.237,
'a1': 0.355,
'a2': -0.769,
'approx': 'lalsim.SEOBNRv2',
'fband': [43.0, 300.0],
'f_min': 10.0}
次に時間、H1の観測データ、L1の観測データそれぞれのデータ数、最小値、平均値、最大値を出していきます。
# H1でもL1でもサンプリングレートは同じであるので、観測時間間隔dtは以下のように定義できる
time = time_H1
dt = time[1] - time[0]
# それぞれのデータ数、最小値、平均値、最大値を求める
print('time_H1: len, min, mean, max = ', \
len(time_H1), time_H1.min(), time_H1.mean(), time_H1.max() )
print('strain_H1: len, min, mean, max = ', \
len(strain_H1), strain_H1.min(),strain_H1.mean(),strain_H1.max())
print( 'strain_L1: len, min, mean, max = ', \
len(strain_L1), strain_L1.min(),strain_L1.mean(),strain_L1.max())
# H1とL1それぞれの観測時間中、使用可能なデータは何秒あるか
bits = chan_dict_H1['DATA']
print("For H1, {0} out of {1} seconds contain usable DATA".format(bits.sum(), len(bits)))
bits = chan_dict_L1['DATA']
print("For L1, {0} out of {1} seconds contain usable DATA".format(bits.sum(), len(bits)))
以下が出力されれば成功です。
time_H1: len, min, mean, max = 131072 1126259446.0 1126259461.999878 1126259477.9997559
strain_H1: len, min, mean, max = 131072 -7.044665943156067e-19 5.895522509246437e-23 7.706262192397465e-19
strain_L1: len, min, mean, max = 131072 -1.8697138664279764e-18 -1.0522332249909908e-18 -4.60035111311666e-20
For H1, 32 out of 32 seconds contain usable DATA
For L1, 32 out of 32 seconds contain usable DATA
ダウンロードしてきたデータの下準備は完了です。
データのことを深いところまで考え出したらキリがないので、ここまではコピペでもいいと思います。
次から実際にプロットしていきます。
スポンサーリンク
予測波形
元々データセットの中にH1とL1での予測波のデータが入っているので、そちらをプロットしてみます。
しかし、この予測波形をプロットするにはこれからやっていく処理等が必要になってくるため、ここではとりあえずグラフだけ貼っておきます。
またあとで予測波形をプロットしてみましょう。
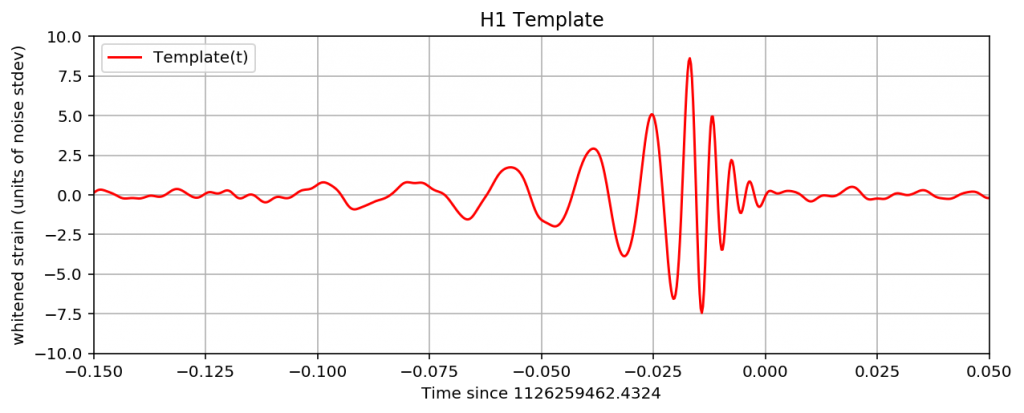
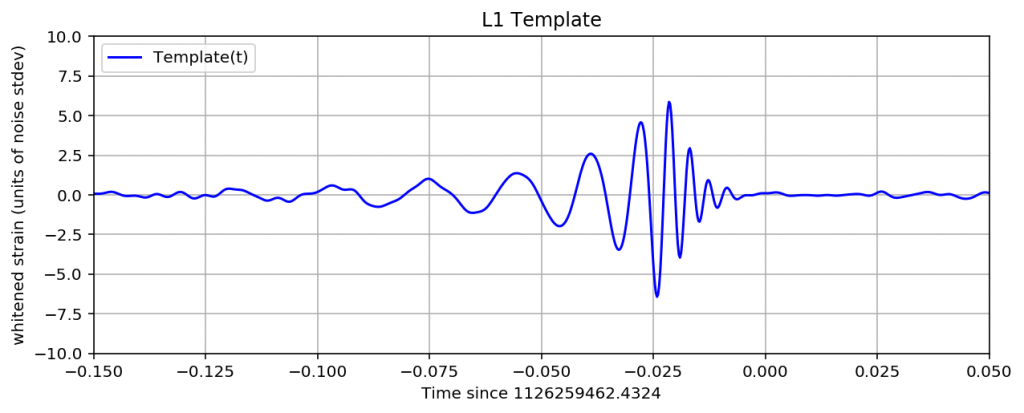
赤がハンフォード、青がリビングストンで観測される重力波の予測波です。
横軸は時間、縦軸は重力波による歪みです。
観測地点が違うので、似ていますが形は少し違うことが分かると思います。
この後、観測データからノイズを除いていきますが、そのゴールとなるのがこの波形です。
観測データのプロット
ここで、実際に観測したデータをプロットしてみましょう。
deltat = 5
indxt = np.where((time >= tevent-deltat) & (time < tevent+deltat))
print(tevent)
def plot_data(use_data,color,use_label):
plt.figure()
plt.plot(time[indxt]-tevent,use_data,color,label=use_label)
plt.xlabel('time (s) since '+str(tevent))
plt.ylabel('strain')
plt.legend(loc='lower right')
plt.title('Advanced LIGO strain data near '+eventname)
plt.savefig(eventname+'_strain.'+plottype)
plot_data(strain_H1[indxt],'r','H1 strain')
plot_data(strain_L1[indxt],'b','L1 strain')
実行すると以下のグラフが出てくると思います。
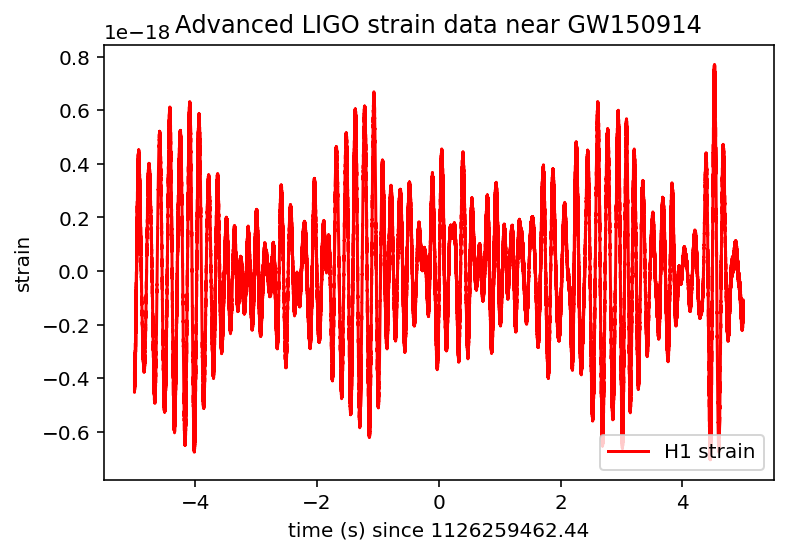
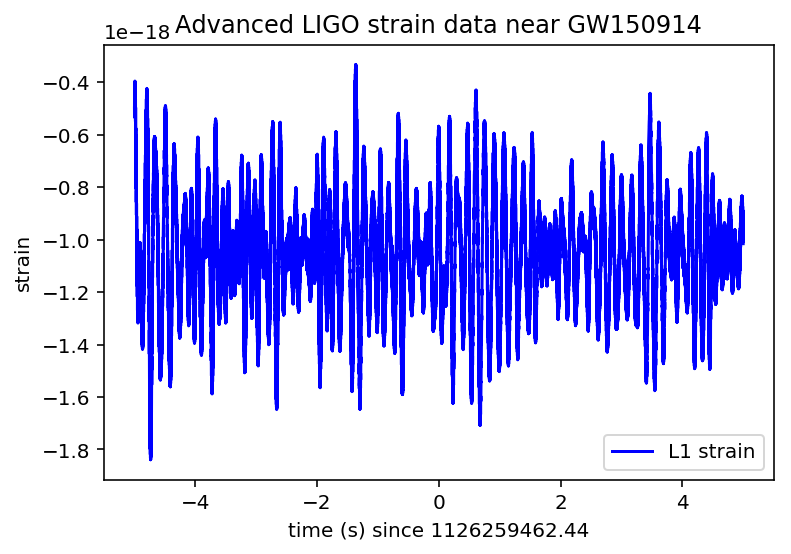
見てみるとあまりにもノイズが大きすぎて重力波が観測できているか全くわかりません。
なのでここからノイズを除いていきます。
スポンサーリンク
振幅スペクトルの計算
振幅スペクトルとは、パワースペクトル密度の平方根をとり、フーリエ変換により周波数ごとに分けた波が各周波数でどれくらいの大きさを持つかを表したものです。
要は各周波数成分がそれぞれどれくらいありますかってことを表したものになります。
これによって明確なノイズの周波数を可視化します。
make_psds = 1
if make_psds:
# 高速フーリエ変換を行う
NFFT = 4*fs #高速フーリエ変換でのサンプル数
Pxx_H1, freqs = mlab.psd(strain_H1, Fs = fs, NFFT = NFFT) #mlab.psdでパワースペクトル密度がすぐに出せる
Pxx_L1, freqs = mlab.psd(strain_L1, Fs = fs, NFFT = NFFT)
# 白色化のために上で計算されたパワースペクトル密度の補間を使う(今回は線形補間)
psd_H1 = interp1d(freqs, Pxx_H1)
psd_L1 = interp1d(freqs, Pxx_L1)
# これはH1の振幅スペクトルを平坦化したもので、後から使う
Pxx = (1.e-22*(18./(0.1+freqs))**2)**2+0.7e-23**2+((freqs/2000.)*4.e-23)**2
psd_smooth = interp1d(freqs, Pxx)
if make_plots:
#振幅スペクトルのプロット
f_min = 20.
f_max = 2000.
plt.figure(figsize=(10,8))
plt.loglog(freqs, np.sqrt(Pxx_L1),'b',label='L1 strain')
plt.loglog(freqs, np.sqrt(Pxx_H1),'r',label='H1 strain')
plt.loglog(freqs, np.sqrt(Pxx),'k',label='H1 strain, O1 smooth model')
plt.axis([f_min, f_max, 1e-24, 1e-19])
plt.grid('on')
plt.ylabel('ASD (strain/rtHz)')
plt.xlabel('Freq (Hz)')
plt.legend(loc='upper center')
plt.title('Advanced LIGO strain data near '+eventname)
plt.savefig(eventname+'_ASDs.'+plottype)
これを実行すると以下のグラフが出力されると思います。
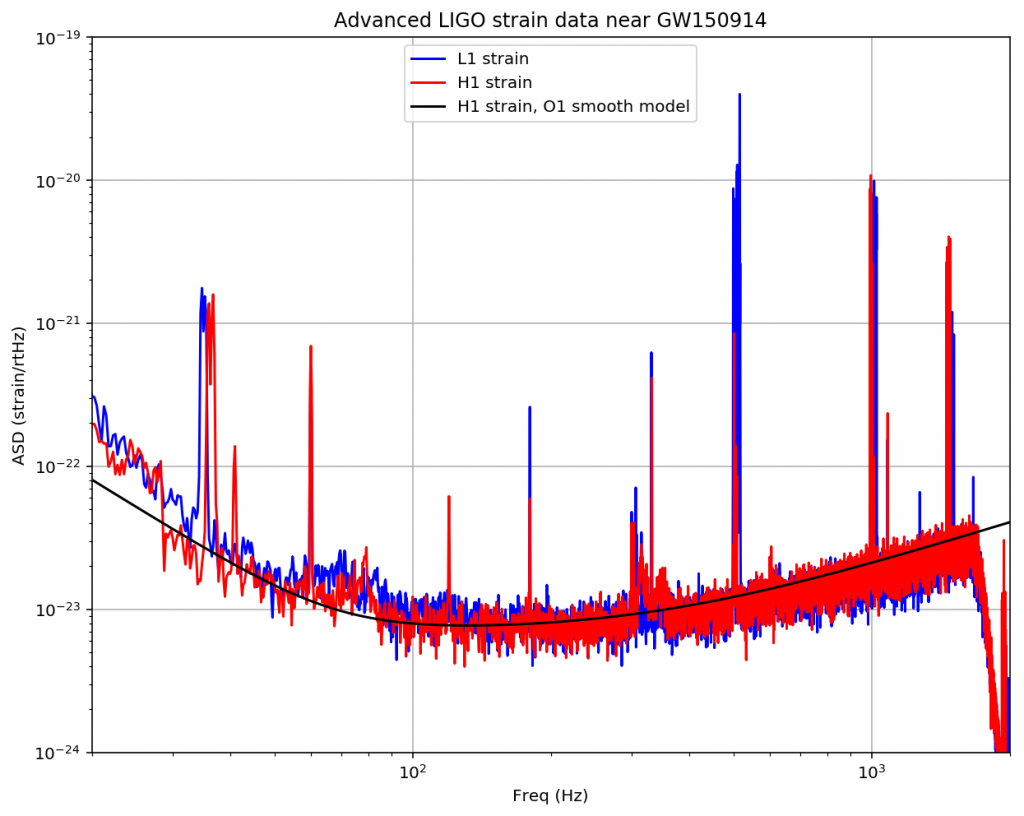
このグラフはどの周波数(横軸)がどれくらい入っているか(縦軸)を表しています。
細く立っているところがシグナルであり、それ以外のところはノイズなのでカットしたいです。
しかし、例えば100Hzちょっとのところにある赤いシグナルですが、振幅スペクトルの大きさとしては20〜30Hzあたりのノイズの方が大きいことが見て分かると思います。
ノイズのカット方法として、単純に全周波数に対してある一定値以下の振幅スペクトルをカットした場合、このようなバックグラウンドで乗っているノイズの大きさのせいで値としては小さくなってしまっているシグナルをカットしてしまう恐れがあります。
そのために白色化を行なっていきます。
また全域に渡っているノイズにも周波数帯によって出現理由が違います。
解析自体には直接関係ありませんが、少し見てみましょう。
低周波数領域・地面振動
低周波領域に現れるノイズは地面振動と呼ばれるものが主となっています。
これはその名の通り地面から来る振動に因るものです。
LIGOの観測機は写真を見てもらえば分かる通り、地面の上に設置されています。
もし地面が揺れてしまえばその振動をモロに受けてしまう可能性があるわけです。
実際LIGOではかなりの地面振動が検出されてしまいます。
先ほどの振幅スペクトルを0Hzからプロットしてみるとわかります。
(このグラフの横軸は対数グラフですので注意してください)
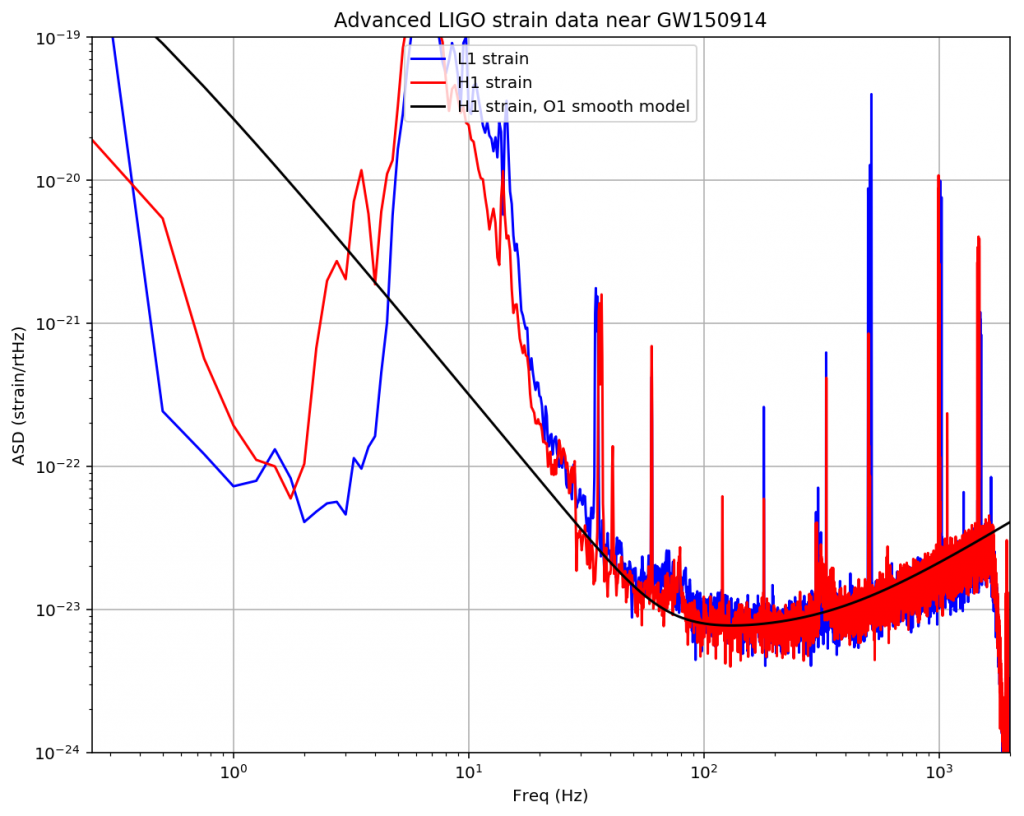
中周波数領域・熱雑音
中周波数領域には熱雑音と呼ばれるものによるノイズが主として出現します。
計器自体も当然何かしらの素材からできているわけですが、この素材の中でのブラウン運動が起きます。
ブラウン運動によって鏡が変形し、ノイズとして現れてしまいます。
高周波数領域・ショットノイズ
高周波領域ではショットノイズというものが生じます。
これは光子数の揺らぎが原因で生じます。
光子のエネルギーが離散的になってしますことが原因で、光子数の平方根に比例する揺らぎが生じます。
スポンサーリンク
白色化
観測データをフーリエ変換によって分解し、振幅スペクトルで割ることで正規化できます。
さらに逆フーリエ変換をして元に戻すことによって、全体に満遍なく広がっているノイズをカットし、一瞬の変化の波を強調させることができます。
def whiten(strain, interp_psd, dt):
Nt = len(strain)
freqs = np.fft.rfftfreq(Nt, dt) #フーリエ変換
freqs1 = np.linspace(0,2048.,Nt/2+1)
hf = np.fft.rfft(strain)
norm = 1./np.sqrt(1./(dt*2))
white_hf = hf / np.sqrt(interp_psd(freqs)) * norm
white_ht = np.fft.irfft(white_hf, n=Nt) #逆フーリエ変換
return white_ht
whiten_data = 1
if whiten_data:
strain_H1_whiten = whiten(strain_H1,psd_H1,dt)
strain_L1_whiten = whiten(strain_L1,psd_L1,dt)
bb, ab = butter(4, [fband[0]*2./fs, fband[1]*2./fs], btype='band')
normalization = np.sqrt((fband[1]-fband[0])/(fs/2))
strain_H1_whitenbp = filtfilt(bb, ab, strain_H1_whiten) / normalization
strain_L1_whitenbp = filtfilt(bb, ab, strain_L1_whiten) / normalization
これで白色化をすることができました。
データをプロット
白色化をしてノイズを除去したデータをプロットしてみましょう。
def output_data(x,data,color):
plt.figure(figsize=(10,8))
plt.subplot(2,1,1)
plt.plot(time-tevent,data,color,label=x+' whitened h(t)')
plt.ylim([-10,10])
plt.xlim([-0.15,0.05])
plt.grid('on')
plt.xlabel('Time')
plt.ylabel('whitened strain (units of noise stdev)')
plt.legend(loc='upper left')
plt.title(x+' whitened data around event')
output_data('H1',strain_H1_whitenbp,'r')
output_data('L1',strain_L1_whitenbp,'b')
これを実行すると以下のグラフが出力されると思います。
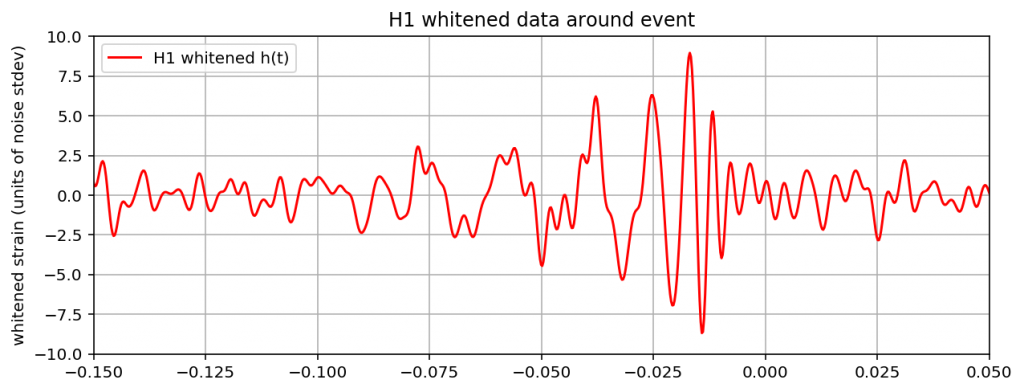
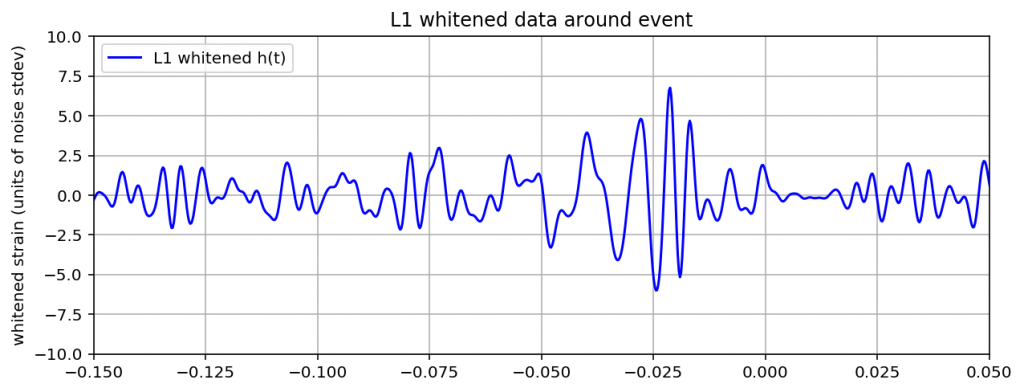
最初の観測生データと比べて、かなり見やすい波形になったと思います。
これらそれぞれに予測波形を重ねて比較してみましょう。
try:
f_template = h5py.File(fn_template, "r")
except:
print("Cannot find template file!")
print("You can download it from https://losc.ligo.org/s/events/"+eventname+'/'+fn_template)
print("Quitting.")
quit()
template_p, template_c = f_template["template"][...]
template_offset = 16.
psd_window = np.blackman(NFFT)
NOVL = NFFT/2
template = (template_p + template_c*1.j)
etime = time+template_offset
datafreq = np.fft.fftfreq(template.size)*fs
df = np.abs(datafreq[1] - datafreq[0])
try: dwindow = signal.tukey(template.size, alpha=1./8)
except: dwindow = signal.blackman(template.size)
template_fft = np.fft.fft(template*dwindow) / fs
dets = ['H1', 'L1']
for det in dets:
if det is 'L1': data = strain_L1.copy()
else: data = strain_H1.copy()
data_psd, freqs = mlab.psd(data, Fs = fs, NFFT = NFFT, window=psd_window, noverlap=NOVL)
data_fft = np.fft.fft(data*dwindow) / fs
power_vec = np.interp(np.abs(datafreq), freqs, data_psd)
optimal = data_fft * template_fft.conjugate() / power_vec
optimal_time = 2*np.fft.ifft(optimal)*fs
sigmasq = 1*(template_fft * template_fft.conjugate() / power_vec).sum() * df
sigma = np.sqrt(np.abs(sigmasq))
SNR_complex = optimal_time/sigma
peaksample = int(data.size / 2)
SNR_complex = np.roll(SNR_complex,peaksample)
SNR = abs(SNR_complex)
indmax = np.argmax(SNR)
timemax = time[indmax]
SNRmax = SNR[indmax]
d_eff = sigma / SNRmax
horizon = sigma/8
phase = np.angle(SNR_complex[indmax])
offset = (indmax-peaksample)
template_phaseshifted = np.real(template*np.exp(1j*phase))
template_rolled = np.roll(template_phaseshifted,offset) / d_eff
template_whitened = whiten(template_rolled,interp1d(freqs, data_psd),dt)
template_match = filtfilt(bb, ab, template_whitened) / normalization
print('For detector {0}, maximum at {1:.4f} with SNR = {2:.1f}, D_eff = {3:.2f}, horizon = {4:0.1f} Mpc'
.format(det,timemax,SNRmax,d_eff,horizon))
if make_plots:
if det is 'L1':
pcolor='g'
strain_whitenbp = strain_L1_whitenbp
template_L1 = template_match.copy()
else:
pcolor='r'
strain_whitenbp = strain_H1_whitenbp
template_H1 = template_match.copy()
def output_data_with_template(x,data,color,template_match):
output_data(x,data,color)
plt.plot(time-tevent,template_match,'k',label='Template(t)')
output_data_with_template('H1',strain_H1_whitenbp,'r',template_H1)
output_data_with_template('L1',strain_L1_whitenbp,'b',template_L1)
少し長いですが、これを実行すれば観測データと予測波を重ねたグラフができます。
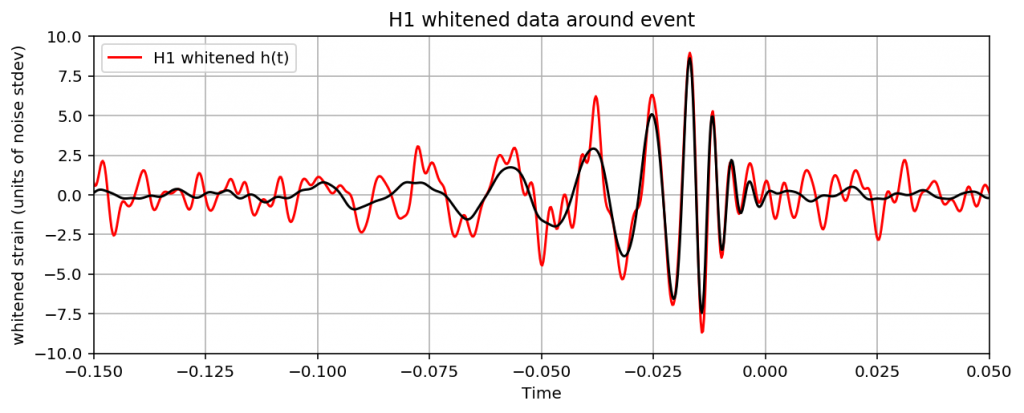
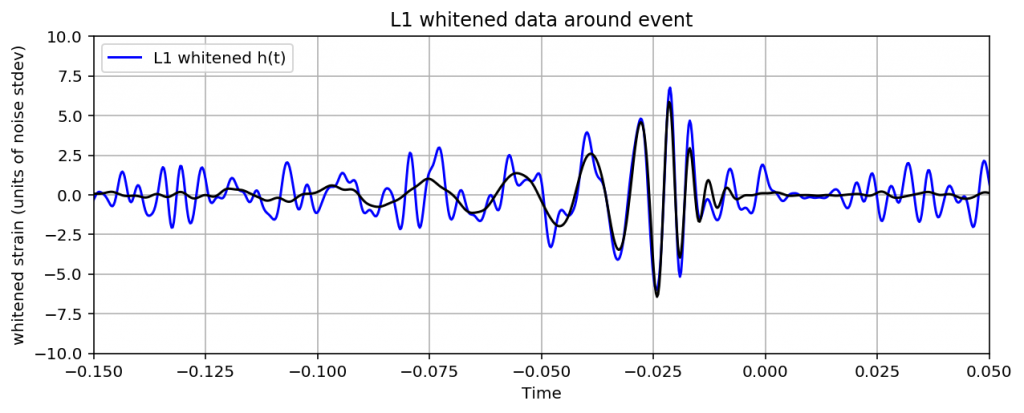
振幅が大きくなっているところで観測データと予測波がかなり合っていることがわかりますね。
これで今回の目標は達成できました!
まだ他にも3つデータがあるので興味があればそちらも解析してみてください。
スポンサーリンク












