名古屋大学大学院理学研究科物理学系・院試解答
2018年度解析力学
問題はこちら
入試データ

解答の訂正等はこちらへお願いします。アドレス：yasketballclub@gmail.com
メールはこちらへ

※スマホ等で見る場合、式が途切れちゃうことがあると思うのでその時は画面を横にして見てください

　

スポンサーリンク

解析力学

問１
角運動量の時間微分を考えて
\begin{eqnarray}
\begin{split}
\bf{\dot{l}}&=&m\bf{\dot{r}} × \bf{v} + m\bf{r} × \bf{\dot{v}}\\
&=& m\bf{v} × \bf{v} + \bf{r} × (-\nabla U)\\
&=&0
\end{split}
\end{eqnarray}
となる。ここで\( \nabla U\)が中心力となることを用いた。

問２
球座標で表した速度ベクトルを２乗する。
\begin{eqnarray}
\begin{split}
\bf{v}^2 =& |(\dot{r}sin\theta cos\phi + r\dot{\theta}cos\theta cos\phi – r\dot{\phi}sin\theta sin\phi ,\\
& \dot{r} sin\theta sin\phi + r\dot{\theta}cos\theta sin\phi + r\dot{\phi}sin\theta cos\phi ,\\
&\dot{r} cos\theta – r\dot{\theta}sin\theta )|^2 \\
=&\dot{r}^2 + r^2 \dot{\theta}^2 + r^2 \dot{\phi}^2 sin^2\theta
\end{split}
\end{eqnarray}

問３
問２より
\begin{eqnarray}
\bf{v}=\dot{r}\bf{e}_r
+r\sqrt{\dot{\theta}^2+\dot{\phi}^2 sin^2\theta}\; \bf{e}_\perp
\end{eqnarray}
と書けるので
\( \bf{r}\)成分は\( v_r=\dot{r}\)、垂直成分は\( v_\perp =r\sqrt{\dot{\theta}^2+\dot{\phi}^2 sin^2\theta}\)となる。
角運動量の大きさは
\begin{eqnarray}
\begin{split}
l=&m\bf{r}× \bf{v}\\
=&mr \cdot r(\dot{\theta}^2 + \dot{\phi}^2 sin^2\theta)^{\frac12}\\
=&mr^2 (\dot{\theta}^2 + \dot{\phi}^2 sin^2\theta)^{\frac12}
\end{split}
となる。
\end{eqnarray}

問４
ラグランジアン
\begin{eqnarray}
L=\frac12 m (\dot{r}^2 + r^2 \dot{\theta}^2 + r^2 \dot{\phi}^2 sin^2\theta)-U(r)
\end{eqnarray}
共役運動量
\begin{eqnarray}
P_r = \frac{\partial L}{\partial \dot{r}}=m\dot{r}
\end{eqnarray}
\begin{eqnarray}
P_\theta = \frac{\partial L}{\partial \dot{\theta}}=mr^2\dot{\theta}
\end{eqnarray}
\begin{eqnarray}
P_\phi = \frac{\partial L}{\partial \dot{\phi}}=mr^2 \dot{\phi}sin^2{\theta}
\end{eqnarray}
これを使えばハミルトニアン
\begin{eqnarray}
H=\frac{{P_r}^2}{2m}+\frac{{P_\theta}^2}{2mr^2}+\frac{{P_\phi}^2}{2mr^2 sin^2 \theta}+U(r)
\end{eqnarray}

問５
問４より
\begin{eqnarray}
\begin{split}
l_z=&m(xv_y – yv_x)\\
=&mr^2 \dot{\phi}^2 sin^2\theta\\
=&P_\phi
\end{split}
\end{eqnarray}
\begin{eqnarray}
\begin{split}
\bf{l}^2=&m^2r^4(\dot{\theta}^2+\dot{\phi}^2sin^2\theta)\\
=&{P_\theta}^2 +\frac{{P_\phi}}{sin^2\theta}
\end{split}
\end{eqnarray}
となる。
よって\( P_\theta=0,\theta=\pi /2\)または\( P_\theta=0,l=P_\phi=0\)のとき\( \bf{l}^2\)と\(l_z \)は一致し
\begin{eqnarray}
\begin{split}
H=\frac{{P_r}^2}{2m}+\frac{l^2}{2mr^2}+U(r)
\end{split}
\end{eqnarray}
または
\begin{eqnarray}
\begin{split}
H=\frac{{P_r}^2}{2m}+U(r)
\end{split}
\end{eqnarray}
となってxy平面上を運動する。

　

スポンサーリンク

問６
\( P_\theta=0,\theta=\pi /2,U(r)=-\frac{k}{r^3}\)のときエネルギー\( E\)は
\begin{eqnarray}
E=\frac{m}{2}\left(\frac{dr}{dt}\right)^2 + \frac{l^2}{2mr^2}-\frac{k}{r^3}
\end{eqnarray}
と表せるので、
\begin{eqnarray}
U_{eff}(r)=\frac{l^2}{2mr^2}-\frac{k}{r^3}
\end{eqnarray}
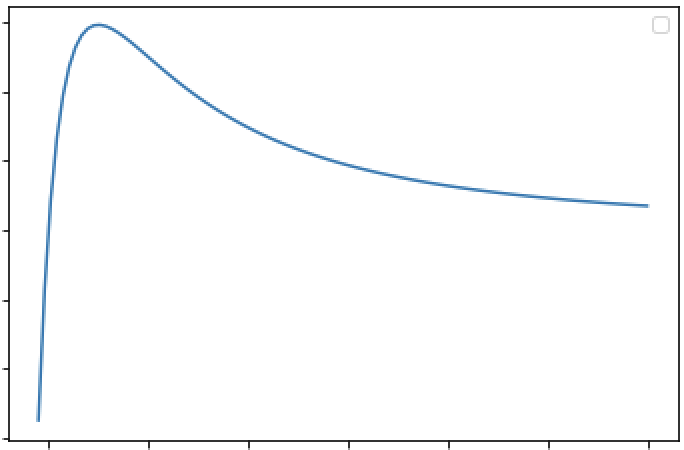
となる。これを微分して0になるのが\( r=r_\ast\)で
\begin{eqnarray}
r_\ast = \frac{3mk}{l^2}
\end{eqnarray}
となる。概形は下図。

• 

問７
無限遠点の運動を考えて、
\begin{eqnarray}
l=mbv_0
\end{eqnarray}
となる。これを\( U_{eff}(r_\ast)\)へ代入して

\begin{eqnarray}
\begin{split}
U_{eff}(r_\ast)&=\frac{(mbv_0)^6}{54m^3k^2}\\
&=\frac{m^3v_0^6}{54k^2}b^6
\end{split}
\end{eqnarray}
となる。問６のグラフより\( U_{eff}(r_\ast)\)を越えることができれば原点へ到達できるので条件は
\begin{eqnarray}
\frac{1}{2}m{v_0}^2&>& \frac{m^3v_0^6}{54k^2}b^6\\
\frac{27k^2}{m^2{v_0}^4}&>& b^6
\end{eqnarray}
つまり臨界値は
\begin{eqnarray}
b_\ast=\sqrt{3}\left( \frac{k}{m{v_0}^2}\right)^{\frac13}
\end{eqnarray}

問８
(1)式より
\begin{eqnarray}
\frac12m{v_0}^2=\frac{m}{2}\left( \frac{dr}{dt}\right)^2
+\frac{l^2}{2mr^2}-\frac{k}{r^3}
\end{eqnarray}
(2)式より
\begin{eqnarray}
\frac{dr}{dt}=\frac{l}{mr^2}\left( \frac{d\phi}{dr}\right)^{-1}
\end{eqnarray}
この２式から
\begin{eqnarray}
\left( \frac{d\phi}{dr}\right)=\left[ \frac{ \frac{m}{2} \left(\frac{l}{mr^2}\right)^2 }{ \frac12m{v_0}^2-\frac{l^2}{2mr^2} + \frac{k}{r^3} }\right]^\frac12
\end{eqnarray}
両辺を\( r\)で積分し
\begin{eqnarray}
\phi =
\int \left[ \frac{ \frac{m}{2} \left(\frac{l}{mr^2}\right)^2 }{ \frac12m{v_0}^2-\frac{l^2}{2mr^2} + \frac{k}{r^3} }\right]^\frac12 dr
\end{eqnarray}

問９
\( \Delta r=r-r_\ast\)として有効ポテンシャルをテイラー展開する。
\begin{eqnarray}
\begin{split}
U_{eff}(r)&=&\frac{l^2}{2m(r_\ast+\Delta r)^2}-\frac{k}{(r_\ast+\Delta r)^3}\\
&\simeq & \frac{l^2}{2m}\left( \frac{1}{r_\ast ^2}-\frac{2}{r_\ast ^3}\Delta r + \frac{3}{r_\ast ^4}\Delta r^2 \right)
-k\left( \frac{1}{r_\ast ^3}-\frac{3}{r_\ast ^4}\Delta r +\frac{3}{r_\ast ^5}\Delta r^2 \right)\\
&=&U_{eff}+\left( -\frac{l^2}{mr_\ast^3} +\frac{3k}{r_\ast^4} \right)\Delta r + \left( \frac{3l^2}{2mr_\ast^4} -\frac{6k}{r_\ast^5} \right)\Delta r^2
\end{split}
\end{eqnarray}
よって
\begin{eqnarray}
\begin{split}
c_1&=& -\frac{l^2}{mr_\ast^3} +\frac{3k}{r_\ast^4}\\
c_2&=&\frac{3l^2}{2mr_\ast^4} -\frac{6k}{r_\ast^5}
\end{split}
\end{eqnarray}
となる。問６の \( r_\ast\)を代入して具体的に計算すると
\begin{eqnarray}
\begin{split}
c_1&=& 0\\
c_2&=&-\frac{l^{10}}{162m^5k^4}
\end{split}
\end{eqnarray}

問１０
有効ポテンシャルや \( b_\ast\)を用い、問８の被積分関数を計算してみる。
\begin{eqnarray}
\begin{split}
\left[ \frac{ \frac{m}{2} \left(\frac{l}{mr^2}\right)^2 }{ \frac12m{v_0}^2-\frac{l^2}{2mr^2} + \frac{k}{r^3} }\right]^\frac12
&\simeq &
\left[ \frac{ \frac{m}{2} (\frac{l}{mr^2})^2 }{ \frac12m{v_0}^2-(\frac12m{v_0}^2- \frac{l^{10}}{162m^5k^4}\Delta r^2 )} \right]^\frac12\\
&=&\frac{9m^2k^2}{l^4}\frac{1}{r^2(r-r_\ast)}
\end{split}
\end{eqnarray}
これで問８の積分は
\begin{eqnarray}
\begin{split}
\phi&=& \left(\frac{3mk}{l^2}\right)^2 \int^r_{r_1} \frac{dr’}{{r’}^2(r’-r_\ast)}\\
&=&r_\ast^2\left[ \frac{1}{r-\ast r’} + \frac{1}{r_\ast^2}ln\left|1- \frac{r_\ast} {r’}\right|\right]^r_{r_1}\\
&=&\frac{r_\ast}{r}-\frac{r_\ast}{r_1}+ln\left|1- \frac{r_\ast} {r}\right|-ln\left|1- \frac{r_\ast} {r_1}\right|
\end{split}
\end{eqnarray}
\( r_\ast\simeq r_1\)であるとすると \( ln\left|1- \frac{r_\ast} {r_1}\right|\)をマクローリン展開して
\begin{eqnarray}
\phi\simeq \frac{r_\ast}{r} + ln\left|1- \frac{r_\ast} {r}\right|
\end{eqnarray}
さらに \( r\)が \( r_\ast\)に近づくときを考えるので \( ln\left|1- \frac{r_\ast} {r}\right|\)もマクローリン展開して
\begin{eqnarray}
\phi\rightarrow \frac{r_\ast^2}{2r^2}
\end{eqnarray}
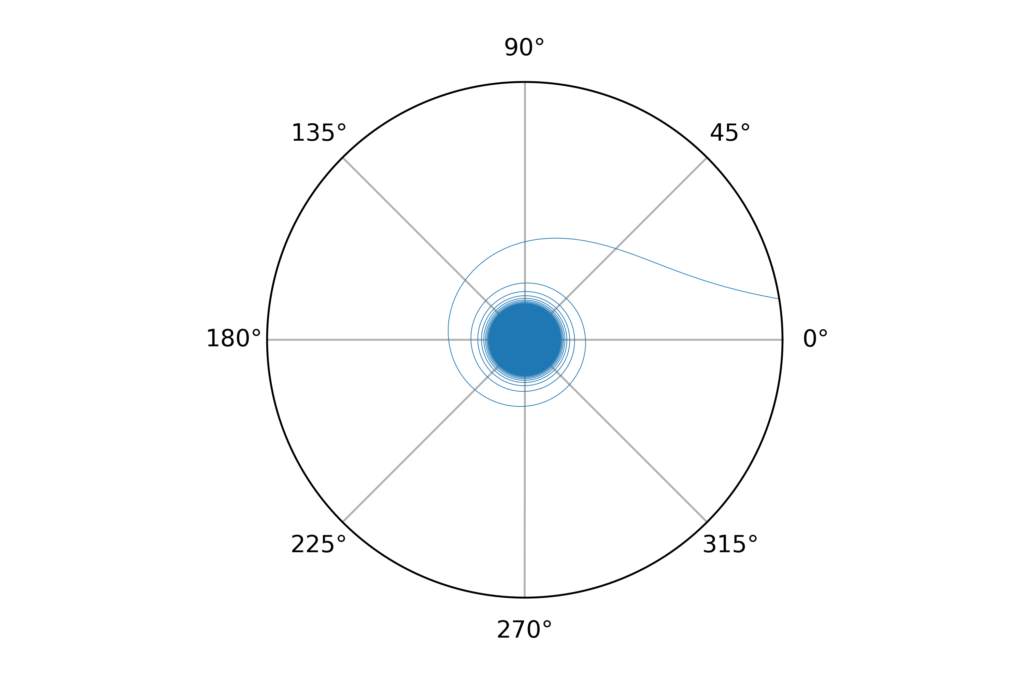
これは \( r\)が小さくなると \( \phi\)が大きくなる、つまりxy平面の中を回転しながら原点に近づくということになる。

概形はこんな感じでしょうか。

• 

真ん中潰れちゃったけど。

　

スポンサーリンク