2020年度名古屋大学の前期課程・物理の解答解説です。

問題はここからとってきてください。

名大2020年度物理

↑掲載期限が切れたようですね。
東進の過去問サイトならいつでも閲覧可能なのでそちら見てもらったほうがいいかもしれません。

、、、難しかった
これを緊張した試験会場で受けた受験生たちは大変だっただろうな、、、

解答の訂正等はこちらへお願いします。アドレス：yasketballclub@gmail.com
メールはこちらへ

※スマホ等で見る場合、式が途切れちゃうことがあると思うのでその時は画面を横にして見てください

　

スポンサーリンク

問題Ⅰ 力学

小問が9個あり、後半は解かせる気ないですね。
よっぽど物理得意な人以外は、(7)以降は明らかな捨て問だと思います。
(6)まではまあまあ一般的な問題だったのでそこでどれだけ解けたかですね。

(1)
合成ばね定数を求めよという問題です.
ばね定数というのは、”バネを単位長さ伸ばすのに必要な力”と理解することができます.
バネ定数\( k\)のばねを２つつなげて単位長さ伸ばそうとすると、それぞれのばねは単位長さの半分伸ばせば良いということになる.
作用反作用を考えればそれぞれのばねにかかる力は引っ張った力と等しいので単位長さ伸ばすのに必要な力は\( \underline{\frac{k}{2}}\).

もちろん合成バネ定数の公式(名前あってる？)によって
\begin{eqnarray}
\frac{1}{k’}&=&\frac{1}{k}+\frac{1}{k}\\
k’&=&\underline{\frac{k}{2}}
\end{eqnarray}
と求めても良い.

(2)
棒への力のつり合いを考えると
\begin{eqnarray}
Mg&=&\frac{k}{2}(5H-S)+k(5H-S)+k(6H-S)\\
S&=&\underline{-\frac{2Mg}{5k}+\frac{27}{5}H}
\end{eqnarray}
となる.

(3)
Pが欲しいので力のモーメントを考えるわけだけども、棒の重心周りのモーメントを考えるのが一番計算がラクなので重心周りで考える.
\begin{eqnarray}
\frac{k}{2}(5H-S)P&=&k(6H-S)Q\\
P&=&\underline{\frac{2Mg+3kH}{Mg-kH}Q}
\end{eqnarray}

(4)
便宜上、まずBが床から離れる時を考えていこう.
Bのばねが自然長になる時が\( t=0\)なので時刻\( t\)でのBのばねの伸びは\( Vt\)である.
時刻\( t_B\)でBの重力とばねの弾性力がつり合うので
\begin{eqnarray}
2Mg-kVt_B&=&0\\
t_B&=&\underline{\frac{2Mg}{kV}}
\end{eqnarray}
である.

次にAが床から離れる時を考える.
Bを考えてやると、時刻\( t=0\)で棒の床からの高さは\( 5H\)である.
Aのばねが自然長の時、棒の床からの高さは\( 5H\)である.
つまり、AとBが自然長になるタイミングは一緒であり、\( t=0\)でAも自然長である.
すると時刻\( t\)でのAのばねの伸びは\( Vt\)であるので、\( t_A\)での力のつり合いを考えると
\begin{eqnarray}
N_A-\frac{k}{2} Vt_A&=&0\\
t_A&=&\underline{\frac{2N_A}{kV}}
\end{eqnarray}

最後にCについて考える.
Cのばねが自然長のとき、棒の高さは\( 6H\)である.
つまり\( t=0\)でCのばねは\( H\)だけ縮んでいる.
よってばねが自然長になる時刻は\( \frac{H}{V}\)
そこからばねが伸び始め\( t_C\)でつり合うので
\begin{eqnarray}
N_C-k V(t_C- \frac{H}{V})&=&0\\
t_C&=&\underline{\frac{N_C}{kV}+\frac{H}{V}}
\end{eqnarray}

(5)
もし、接着が無かったとすると、Aが床から離れる時刻は力のつり合いより
\begin{eqnarray}
Mg-\frac{k}{2}Vt_B&=&0\\
t&=&\frac{2Mg}{kV}
\end{eqnarray}
となる.
これがAが床から離れる時刻の最速となる.
これは(4)より\(t_B \)と等しく、接着している状態ではもっと時間がかかるため\( \underline{ア}\)

(6)
最初重心は高さ\( \frac32 H\)にあり、浮くことで毎秒\( V\)ずつ上がっていく.
よって
$$z=\underline{\frac32 H +V(t-\frac{2Mg}{kV})}$$

ここからが頭おかしい.
受験生はここからは捨てていいと思う.



(7)
この問題の何がめんどくさいかというと、Aが単振動しているということです.

今、\( N_A\)が\( 3Mg\)だと言っているので、(6)で求めた\( t_A\)は\( \frac{6Mg}{kV}\)だと分かります.
これは(5)で考えた接着が無い時の\( t_A\)よりも大きくなっているので、Aはばねがつり合いの長さよりも長くなっているときに床から離れます.

なのでこの時Aはビョンビョン単振動していることが分かります.



、、、、、やる気無くなりますね.

まあ頑張ってAの単振動を求めていきましょう.

まず、AとBはつり合いの位置が同じでしたので、Aのつり合いの位置は自然長から\( \frac{2Mg}{k}\)です.

また、\( t_A=\frac{6Mg}{kV}\)ですので、時刻\( t_A\)までに\( \frac{6Mg}{k}\)ばねが伸びていることがわかる.

つまりAの単振動はつり合いの位置を中心に振幅は\( \frac{4Mg}{k}\)となっている.

この単振動の角振動数は運動方程式立てればわかって\( \sqrt{\frac{k}{2M}}\)である.
振幅MAXの状態から単振動が始まっているので単振動はcos型で書け、自然長からの伸びは
$$x(t)=\frac{2Mg}{k} +\frac{4Mg}{k}cos(\sqrt{\frac{k}{2M}}(t-t_A))$$である.

以上よりAばねからかかる力は
$$\frac{k}{2} x(t)=Mg +2Mgcos(\sqrt{\frac{k}{2M}}(t-\frac{6Mg}{k}))$$
となります.

次にBについて考えます.
Bはつり合いの位置で床から離れているので単振動はしていません.
なので時間に関わらずばねの伸び\( \frac{2Mg}{k}\)分の弾性力がはたらきます.
よってBからはたらく力は\( 2Mg\)

Cはまだ地面と接着しているので、時間に伴い伸びていくばねの弾性力がはたらきます.
時刻\( t\)での棒の高さは\( 5H+Vt\)ですので、ここからばねの自然長\( 2H\)とCの大きさ\( 4H\)を引いたものに\( k\)を掛けたら弾性力になります.
したがってCからはたらく力は\( k(Vt-H)\)

最後に棒の重力もありますので\( Mg\)

これらを全部足すと
$$4Mg+2Mgcos(\sqrt{\frac{k}{2M}}(t-\frac{6Mg}{k}))+k(Vt-H)$$
となります.
ここで解答欄を見てやるとsinで書けということなので、位相を\( \frac{\pi}{2}\)ずらしてやって
$$\underline{4Mg+2Mgsin(\sqrt{\frac{k}{2M}}(t-\frac{6Mg}{k})+\frac{\pi}{2})+k(Vt-H)}$$

(8)
\( 0\leq t \leq t_A\)の間にした仕事を考えるのでそれぞれの力学的エネルギーを比較し、その差分が仕事ということになる.

力学的エネルギーを比較するわけだけども、棒の運動エネルギーは常に一定なので以下では考えない.

まず\( t=0\)のとき
・運動エネルギー
AもBもCも床に接しているので0

・位置エネルギー
ブロックたちは全て床に接しているのでこの位置をそれぞれの基準位置としよう.
また、棒の位置も\( t=0\)を基準位置としよう.
よって全て0.

・弾性エネルギー
AとBのばねは自然長であるので0
CはHだけ縮んでいるので\( \frac{1}{2}kH^2\)

よって\( t=0\)での力学的エネルギーは\( \frac{1}{2}kH^2\)である.

\( t=t_A\)のとき
・運動エネルギー
このときAとBが速度\( V\)で動き出すのでそれぞれ\( \frac{1}{2}MV^2\)と\( MV^2\)
Cは床と接着しているので0.

・位置エネルギー
\( t=t_A\)までに棒は\( \frac{6Mg}{k}\)上昇するので位置エネルギーは\( \frac{6M^2g^2}{k}\).
また、棒が\( \frac{6Mg}{k}\)上昇してBのばねのつりあいの位置が\( \frac{2Mg}{k}\)なのでBの上昇は\( \frac{4Mg}{k}\).
よってBの位置エネルギーは\( \frac{8M^2g^2}{k}\).

・弾性エネルギー
\( t=t_A\)でAは床から外れているのでこの時までばねは伸び続けている.
(7)より\( \frac{6Mg}{k}\)伸びているので、Aのばねの弾性エネルギーは\( \frac{9M^2g^2}{k}\)

(7)より、Bのばねは常に\( \frac{2Mg}{k}\)だけ伸びているので、Bのばねの弾性エネルギーは\( \frac{2M^2g^2}{k}\).

Cのばねも(7)より\( (Vt_A-H)\)伸びているので、Cのばねの弾性エネルギーは\( \frac{1}{2}k(\frac{6Mg}{k}-H)^2\).

よって\( t=t_A\)の力学的エネルギーは
$$\frac{43M^2g^2}{k}-6MgH+\frac32 MV^2 +\frac12 kH^2$$
となる.

よって差分は
$$W=\underline{\frac{43M^2g^2}{k}-6MgH+\frac{3}{2} MV^2}$$

(9)
共振は振動の角振動数による.
角振動数は(7)で求めた通り\( \underline{\sqrt{\frac{k}{2M}}}\cdots (お)\)

振動中心は時間とともに上昇する.
よってアは除外.

共振は振動の振動数と固有振動数が近いことによって振幅が増大することである.
よって角振動数は変わらないので答えは\( \underline{イ}\cdots (か)\)

これでやっと大問１つ終わりました。
誰が解けるんじゃいこんなん

　

スポンサーリンク

問題Ⅱ 電磁気学

難易度は設定が見慣れないけど力学に比べればまだマシ。
けど入試物理としてはかなり難しい部類に入るのではないかと思います。
誘導はかなり丁寧で前問の答えとか使いまくるので、その誘導に気付けるかどうかですな。

(1)
コイル一辺の長さは \( \frac{\sqrt{2}}{2}d\).
回路に流れる電流はオームの法則で\( \frac{E}{R}\)
それが並列になっているコイルに流れ込むのでコイル一辺に流れる電流は$$\underline{ \frac{E}{2R}}$$
よってそれぞれの辺が受けるローレンツ力は \( \frac{\sqrt{2}EBd}{4R}\).
レールに垂直な成分は打ち消しあうので、レールと平行な成分だけ残り
$$ \frac{\sqrt{2}EBd}{4R}cos45°=\frac{EBd}{4R}$$
４辺あるのでコイル全体が磁場から受ける力は
$$\underline{\frac{EBd}{R}}$$
これが\( Mg\)とつり合っているので
$$M=\underline{\frac{EBd}{gR}}$$

(2)
一辺の誘導起電力の大きさは \( \frac{vBd}{2}\).
よって電流はオームの法則より
$$I=\underline{\frac{vBd}{2R}}$$
右ねじの法則を考えれば流れる向きはP→Cなので \( \underline{ア}\).

(3)
抵抗を流れる電流は(2)の２倍なので \( \frac{vBd}{R}\).
コイルはコイルは起電力 \( vBd\)の電池が並列に並んでいると考えられる.
よって
\begin{eqnarray}
W&=&IV\\
&=&\underline{\frac{v^2B^2d^2}{R}}
\end{eqnarray}

(4)
一辺のコイルがレールと平行方向に受けるローレンツ力は
$$\frac{vBd}{2R}×B×\frac{\sqrt{2}d}{2}cos45°=\frac{vB^2d^2}{4R}$$
４辺あるので \( \frac{vB^2d^2}{R}\)
\( v_0\)のときこれが\( Mg=\frac{EBd}{R}\)とつり合う.
なので
$$v_0=\underline{\frac{E}{Bd}}$$

(5)
(1)よりこの時コイルが受ける力は \( \frac{EBd}{R}\).

次に磁石が受ける力を考える.
磁石が磁場から受ける力は上向きを正とするとN極では \( \frac{mB}{μ}\)、S極では \(- \frac{mB}{μ}\).
よって磁石が受ける力は打ち消しあう.
なのでこの場合磁石にかかる力は重力だけとなる.

以上よりコイルにはたらくローレンツ力と磁石の重力\( M_1g\)が釣り合っていることになるので
$$M_1=\underline{\frac{EBd}{gR}}$$

(6)
磁場に勾配がある状態で、磁場から磁石にかかる力を考える.
N極にかかる力は
$$\frac{mB}{μ}+\frac{K\Delta z_N m}{μ}$$
S極にかかる力は
$$-\frac{mB}{μ}-\frac{K\Delta z_S m}{μ}$$
よって磁石にかかる力は
$$\frac{Km}{μ}(\Delta z_N-\Delta z_S)$$
となる.
\( \Delta z_N-\Delta z_S\)は \( l\)であるのでかかってる力は
$$\frac{Kml}{μ}$$
となる.

レールに対して静止しているので磁石にかかる重力と磁場から受ける力がつり合っていることになる.
\begin{eqnarray}
\frac{EBd}{R}&=&\frac{K_0ml}{μ}\\
K_0&=&\underline{\frac{μEBd}{mlR}}
\end{eqnarray}

(7)
速度 \( v_1\)で動いている時刻\( t_1\)での力学的エネルギーと静止した時の力学的エネルギーを比較し、減っている分が抵抗で消費されたジュール熱ということになる.

時刻\( t_1\)での状況は(4)の状況と同じため、\( v_1=\frac{E}{Bd}\)

ここで、(6)より磁石が磁場から受ける力と磁石の重力が反対向きに同じ大きさであることがわかる.
従って時刻\( t_1\)から静止するまでに重力がした仕事と磁場から受ける力がした仕事が打ち消しあう.

よって考える力学的エネルギーは運動エネルギーだけで良く、時刻\( t_1\)での運動エネルギーが抵抗で消費されたジュール熱となる.

(1)(5)より \( M,M_1\)は共に \( \frac{EBd}{gR}\)であるので、
\begin{eqnarray}
W&=&\frac{1}{2}(M+M_1)v_1^2\\
&=&\underline{\frac{E^3}{gRBd}}
\end{eqnarray}

　

スポンサーリンク

問題Ⅲ 波動

(1)
d離れた点Aに伝わる波は$$\underline{\frac{2\pi \lambda}{d}}\cdots (あ)$$だけ位相が遅れる.
AとBの波は同位相なのでdが波長の整数倍であれば強め合う.
\begin{eqnarray}
d&=&n\lambda\\
\lambda &=&\underline{\frac{d}{n}}\cdots (い)
\end{eqnarray}
今度は逆位相なのでBの波はAで半波長ぶんズレていれば良い.
\begin{eqnarray}
d&=&(m+\frac12)\lambda\\
\lambda &=&\underline{\frac{d}{m+\frac12}}\cdots (う)
\end{eqnarray}
AからOMへ垂線をおろし、その点をPとすると \( \angle B=\phi, \angle P=90°\)の直角三角形APBができる.
\( PB=|MA-MB|\)であるので
$$PB=dcos\phi$$
\( dcos\phi\)で位相が半波長分ズレればいいので
\begin{eqnarray}
dcos\phi&=&(a+\frac12)\lambda\\
&=&(a+\frac12)\frac{d}{(m+\frac12)}
\end{eqnarray}
なので
$$(2m+1)cos\phi=2a+1$$
となり答えは\( \underline{コ}.\cdots (お)\)

この次は捨て問でいいと思います.

これはmを指定してやれば、aの値によって強め合う\( \phi\)を決定できる式である.
\( m=1\)のとき
$$cos\phi =\frac{2a+1}{3}$$
であり\( a=1\)のとき\( cos\phi=1\)に対応する.
\( cos\phi\)は\( 0 \leq \phi \leq \frac{\pi}{2}\)で減少関数なので、次に強め合うのは\( a=0\)のときの\( cos\phi =\frac{1}{3}\)のときになる.
この\( cos\phi =\frac{1}{3}\)を知っているcosの値によって評価する.
\( cos\frac{\pi}{3} =\frac{1}{2}, cos\frac{\pi}{2} =0\)であるので
$$cos\frac{\pi}{2} < \frac13 = cos\phi < cos\frac{\pi}{3}$$ $$\frac{\pi}{3} < \phi< \frac{\pi}{2}$$ $$0.333\cdots \pi<\phi<0.5\pi$$ となるので選択肢見てやって当てはまるのはまあギリ \( \underline{キ}\cdots (か)\)かなと.

(か)に関してはとっさにこの考え方が思いつけば出来るかもしれないけど、試験会場では思いつかないのでは.
実際の試験でもテキトーに選択肢選んだ人が大半かなと思います.



(2)はほぼ捨て問です。
(き)(く)とかだけやってあとは逃げればいいと思います。
この問題使って練習する時は、幾何の解法の引き出しが増えればいいかなと思います。

(2)
Dから垂線をおろし直角三角形を作る。
すると
$$|MB-MD|=qsin\phi$$
となり同様に考えれば
$$|MB-MA|=qcos\phi$$
となる.
こんな感じの図を考えれば(雑でスマン)

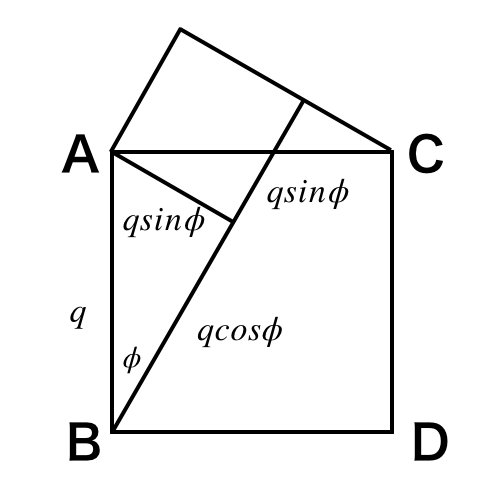
$$|MB-MC|=q(cos\phi +sin\phi )$$
となることがわかる.
\( tan\phi = \frac12\)なので
$$cos\phi = \frac{2}{\sqrt{5}}$$
$$sin\phi = \frac{1}{\sqrt{5}}$$
であるので、
$$|MB-MD|=\underline{\frac{1}{\sqrt{5}}q}\cdots (き)$$
$$|MB-MA|=\underline{\frac{2}{\sqrt{5}}q}\cdots (く)$$
$$|MB-MC|=\underline{\frac{3}{\sqrt{5}}q}\cdots (け)$$
となる.
全ての点の間隔が波長の整数倍となれば強め合うので、(き)(く)(け)を眺めれば全て\({\frac{1}{\sqrt{5}}q \)の整数倍であることがわかる.
よって
$$n\lambda=\frac{1}{\sqrt{5}}q$$
$$\lambda=\underline{\frac{1}{\sqrt{5}n}q}\cdots (こ)$$
次に\( tan\phi = \frac14\)になったので上と全く同様に考えてやると
$$|MB-MD|=\underline{\frac{1}{\sqrt{17}}s}\cdots (き)$$
$$|MB-MA|=\underline{\frac{2}{\sqrt{17}}s}\cdots (く)$$
$$|MB-MC|=\underline{\frac{3}{\sqrt{17}}s}\cdots (け)$$
なので
$$n\lambda=\frac{1}{\sqrt{17}}q$$
$$\lambda=\underline{\frac{1}{\sqrt{17}n}q}\cdots (さ)$$
図５を45°傾けると格子間隔が\( \frac{s}{\sqrt{2}\)になった図４になることがわかる.
よって上の考えをs→\( \frac{s}{\sqrt{2}\)、\( \phi\)→\( \phi + \frac{\pi}{4}\)で考えてやると
$$|MB-MD|=\frac{5}{2\sqrt{17}}s$$
$$|MB-MA|=\frac{3}{2\sqrt{17}}s$$
$$|MB-MC|=\frac{8}{2\sqrt{17}}s$$
波長が\( \frac{1}{2\sqrt{17}}s\)の整数倍であればいいので
$$\lambda=\frac{1}{2\sqrt{17}n}q$$
\( n’=2n\)とおくと正数nに対してn’は偶数となる.
よって(さ)の式で強め合うnは偶数、すなわち\( \underline{エ}\cdots (し)\)

まとめ

問題としては全体的に面白いと思います。
ただこの難易度の問題を普通の受験生が50%得点できるかと考えたらビミョいんじゃないかと思います。
この問題出すならせめて75分よりも試験時間伸ばしてあげないと厳しいんじゃないかな、、、、、

結論

鬼


　

スポンサーリンク